

![[Previous Page]](prev.gif)
![[Next Page]](next.gif)
![[Up]](up.gif)
![[Home Page]](home.gif)
![[Mail]](mail.gif)
![[Contents]](contents.gif)

What is a scale?
A scale is a subset of all tones in an octave.
This sounds pretty theoretical, but describes the nature of all scales that are played in any kinda music. As you might know there are even quartertones in some oriental scales.
Ok, back to "reality". Occidental music is made from semitones and there are 7 different semitones in the most common scales like the major or the minor scale.
The nature of scales can be explained best with the help of the piano keyboard. Please keep in mind that playing scales in different keys is easier on guitar than on most other instruments.

First let's explore the C major scale. That's the most simple scale on the piano keyboard, because it consists out of only the white keys.
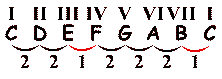
So, what is this all about?
The nature of a certain sort of scale are the distances between it's tones. It's a whole step (two semi tones) between the C (I) and the D (II), a whole step between the D (II) and the E (III), a half step (one semi tone) between the E (III) and the F (IV) and so on. The half steps are marked above.
If you need to figure out the notes that form a (Ionian) major scale in another key, you just have to make sure that the distances between the notes I, II, III, IV, V, VI, and VII are the same like above.
This is called transposing. It's easy on guitar, it's more difficult on a piano and it's pretty difficult on wind instruments.
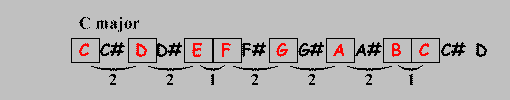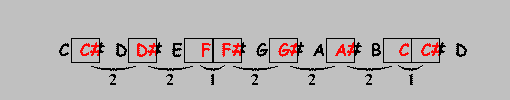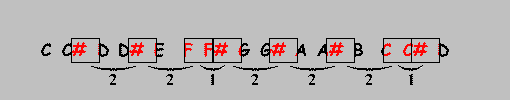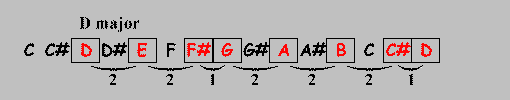
The boxes in the animation above form the pattern of the (Ionian) major scale and when you transpose that scale the pattern remains the same, the notes marked by them change, though.
The result is that the D major scale consists out of the notes D, E, F#, G, A, B and C#.
That's why transposing on a guitar is so easy. The fingering patterns of scales or chords remain the same, you just have to move them up or down the fretboard.
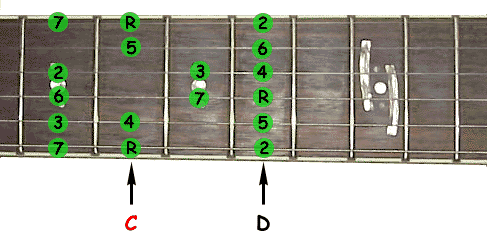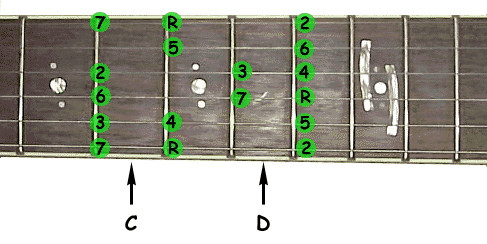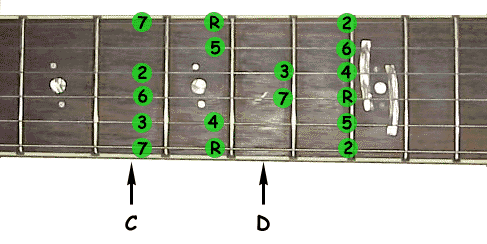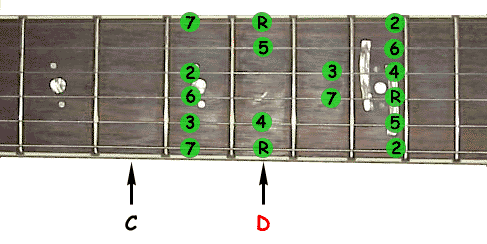
The animation above shows how a fingering pattern is transposed to another scale. Here it is the C major scale we were talking about before that is transposed to D major. The root note (the actual key) is marked with an "R", the numbers represent the notes of the scale. Transposing the scale to another key than D works analogous. Just make sure that the root note is positioned on the root note of the desired key.
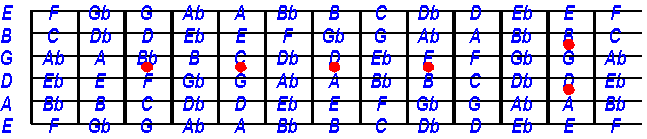
Here is a mpa of the keyboard that helps you to position all fingering patterns.
What is the difference between major and minor scales?
Now, that's actually pretty easy.
The interval between the root note and the 3rd note is a major 3rd (4 semitomes), that between the root and the 3rd of a minor scale is a minor 3rd.
This implies that there are different kinds of major scales and different kinds of minor scales. More about that later.
The pattern of a classic (Aeolian) minor scale looks like this:

There is a distance of 2 + 1 = 3 semitones between the root note (A) and the 3rd (C). That's a minor 3rd, like I have mentioned before.
Again I have picked the most simple (Aeolian) minor scale (A minor) that can be played on a piano keyboard. One that only consists out of white keys.
It is pretty obvious that the (Ionian) C major scale and the (Aeolian) A minor scale are kinda relatives. The both consist out of the same set of note (only white keys).
Which other scales can be derived from the C major scale?
To figure that out, we take the notes of the C major scale and build another scale on each note using the given notes.

The resulting scales are called modes of the original scale. In this case they even have names. They are named after some ancient triebes, because those triebes were using them for playing their music.
Another thing that is kinda remarkeable is that the modes are either some kind of major or minor scale - the distance between the root and the 3rd note is either a major 3rd (4 semi tones) or a minor 3rd (3 semi tones). The Locrian mode contains a diminished 5th (1+2+2+1=6 semi tones) , all others have a normal 5th (7 semi tones).
Now we have figured out the different modes, which resulted in different major and minor scales. But what is this all good for?
Let's go a step further and build a chords out of each of theose modes. That will result in chords that are kinda relative chords, look at them like they are members of a family.
| Mode | Chord | General |
| Ionian | Cmaj7 | Imaj7 |
| Dorian | Dm7 | IIm7 |
| Phrygian | Em7 | IIIm7 |
| Lydian | Fmaj7 | IVmaj7 |
| Mixolydian | G7 | V7 |
| Aeolian | Am7 | VIm7 |
| Locrian | Bm7/b5 | VIIm7/b5 |
So, now we have families of chords and scales, but what does that help in real life?
Quite a bit! Usually music pieces have chord progressions of which parts (or even the whole piece) consist of chords that belong to one family. That sounds good and you can use the same notes for improvising over that parts or the whole piece.
So if you have a progression that looks like
Dm7 - G7 - Cmaj7 (IIm7-V7-Imaj7).
you can play the Cmajor scale over it and don't have to change the scale you use for improvising on each chord.
A pretty common progession is
Fmaj - G7 - Cmaj (IV-V7-I)
Look it up in the table above and you can see, that you can use the C major scale to improvise on it, too. BTW: You can always leave out the 7th of the chords above.
Of course the modes are not only existing for the C major scale. You can easily transpose it to all other keys.
E.g. you can play the Ab major scale on Bbm7 - Eb7 - Abmaj7 that's the IIm7-V7-Imaj7 in the Ab major key.
You can also do the same kind of analysis for other kinds of scales like the harmonic minor scale and the result will be another family of chords on which you can use a harmonic minor scale.
Ok, to reapeat what we have done before, we do it once again for A harmonic minor.
That the different between that scale and the ordinary aeolian minor it the major 7th instead of the normal 7th in it. So it contains a G# instead of the G.
The notes are:
A - B - C - D - E - F - G# - A

Now we have determined the modes of the harmonic minor scale. Actually I dunno how to name them, AFAIK there is no common way to do so.
It is obvious that we can use the A harmonic mainor scale to improvise on a pretty common progression that is
Bm7/b5 - E7 - Am(maj7) (IIm7/b5-V7-Im)
That is a diminished II-V-I which occures in many jazz pieces, too.
Another interesting scale to be analyzed like that is the melodic minor scale. But that's your homework. Especially the 7th mode of the scale is a pretty interesting one. It's the so called altered scale, which is usefull on dominant 7th chords that lead to their tonic.
In the A melodic minor scale a F# replaces the F of the harmonic minor scale, the rest is same like the harmonic minor scale.
Just take the scale, write it down like above, cycle it through the 7 modes, write down the semitone steps between the notes (like above) and cycle that through the modes, too. Then determine the chords that can be built on each mode. That means mark the 3rd, 5th and 7th and determin wether they are a minor or major third, a diminished, normal or augemted 5th and a 6th, 7th or major 7th.
Do that for every mode.
And what's about arpeggios and pentatonics?
An arpeggio is just a subset of a scale. That's the notes that are contained in the chord you can built on the root of a certain scale/mode (the root, 3rd, 5th and 7th). All other notes are not part of the arpeggio.
Why is it a good idea to know the arpeggios? Well, when you improvise, you can do pretty wild and dissonant things like playing "out", the more dissonant, the more tension you produce. But the tension belongs in the middle of a phrase. A good solo kinda breathes, there is a repeating change between tension and release (consonant). At the beginning and the end of a phrase there should be a consonant tone. The tones that form the chord you end your phrase on are the most consonant tones possible. That's what an arpeggio is good for, just a bunch of notes that always fit.
And what's about pentatonics?
That's another subset of the scale, that produces more tension than the arpeggio, but less than the whole scale. Just exclude the notes that produce the half steps.
In a (Ionian) major scale the half steps are between the 3rd and the 4th and between the 7th and the root. The 3rd is a useful (consonant) note, so we exclude the 4th, the root is always a good choice to be kept, so we exclude the 7th.
So we have the root, 2nd, 3rd, 5th and 6th that form a major pentatonic scale. That are 5 notes (penta = five) so now we know why it is called pentatonic.
It's the same with the pentatonic on the Mixolydian mode, just exclude the 4th and the 7th.
The pentatonic on the Dorian or Aeolian mode is formed by the root, 3rd, 4th, 5th and 7th.
What else to say about scales and soloing?
This website can only give you an idea of what soloing is all about. There are plenty books written about it nad if you are interested, just get one.
There are pretty wild things like playing a C# minor pentatonic on a C7 chord. That doesn't seem to fit, but when you have analyzed the relation of each note of that clare to the C7 chord, it looks pretty logic, that are all notes that fit into an altered C7 chord (b9, maj 3rd, #11th, b13th, maj7th).
Finally every semi tone has a relation to a chord and will sound good if it is played in the right context (Remember the tension/release thing?).
Actually you can play everything, you just have to make it sound good anyhow.
A not very helpful statement, huh?

| [Previous] | How to continue... |
| [Next] | Circle of the fifth |
| [Up] | Some Music Theory |
| [Home] | Home Page |
| [Mail] | Send EMail to Sven's Guitar Site |
| [Contents] | Sven's Guitar Site Contents |

Last modified on Monday, 25. September 2017